ユニバーサルジョイントの3つの軸が同一平面上にない場合の解析の基本的考え方を前回明らかにしました。3つの軸が同一平面上にある場合は、作図によって角度等の関係の式を簡単かつ直感的に求めることができますが、そうでない場合は、3次元空間で軸の位置を考える必要があり、作図して求めるには困難が予想されます。
作図に頼らずに機械的に計算ができるよう、以下に説明するベクトルに関する2つの概念を用いることとします。いずれも数学の基礎的な概念ですので、いろいろな説明がネット上に存在します。必要に応じて検索していただき、わかりやすい説明があれば、そちらもご確認ください。
まず、ベクトル\(\vec{a}=(a_x,a_y,a_z)\)と、ベクトル\(\vec{b}=(b_x,b_y,b_z)\)とのなす角度\(\theta\)に関して次の関係が成り立つことを利用します。ただし、\(0\le\theta\le\pi\)とします。
\(cos(\theta) = \frac{{a_x}\cdot{b_x}+{a_y}\cdot{b_y}+{a_z}\cdot{b_z}}{\sqrt{{a_x}^2+{a_y}^2+{a_z}^2}\cdot\sqrt{{b_x}^2+{b_y}^2+{b_z}^2}}\)
ベクトル\(\vec{a}=(a_x,a_y,a_z)\)と、ベクトル\(\vec{b}=(b_x,b_y,b_z)\)との内積が
\(\vec{a}\cdot\vec{b} = a_x\cdot b_x + a_y\cdot b_y + a_z\cdot b_z\)
であること、ベクトル\(\vec{a}=(a_x,a_y,a_z)\)の長さ\(|\vec{a}|\)は内積演算を用いると
\(|\vec{a}| = \sqrt{\vec{a}\cdot\vec{a}}\)
であることを利用すれば、上記の式は
\(cos(\theta) = \frac{\vec{a}\cdot\vec{b}}{|{\vec{a}}|\cdot|{\vec{b}}|}\)
と表すこともできます。
次に、ベクトルの外積という概念を利用します。\(\vec{A}=(a_x,a_y,a_z)\)と、ベクトル\(\vec{B}=(b_x,b_y,b_z)\)とがあったときに、次の計算で得られるベクトル\(\vec{A}\times\vec{B}\)を\(\vec{A}\)と\(\vec{B}\)との外積ベクトルと呼びます。この外積ベクトルは\(\vec{A}\)と\(\vec{B}\)との両方に垂直であるという重要な性質を持ちます。
\(\vec{A}\times\vec{B} = (a_y\cdot b_z - a_z\cdot b_y, a_z\cdot b_x - a_x\cdot b_z, a_x\cdot b_y - a_y\cdot b_x)\)
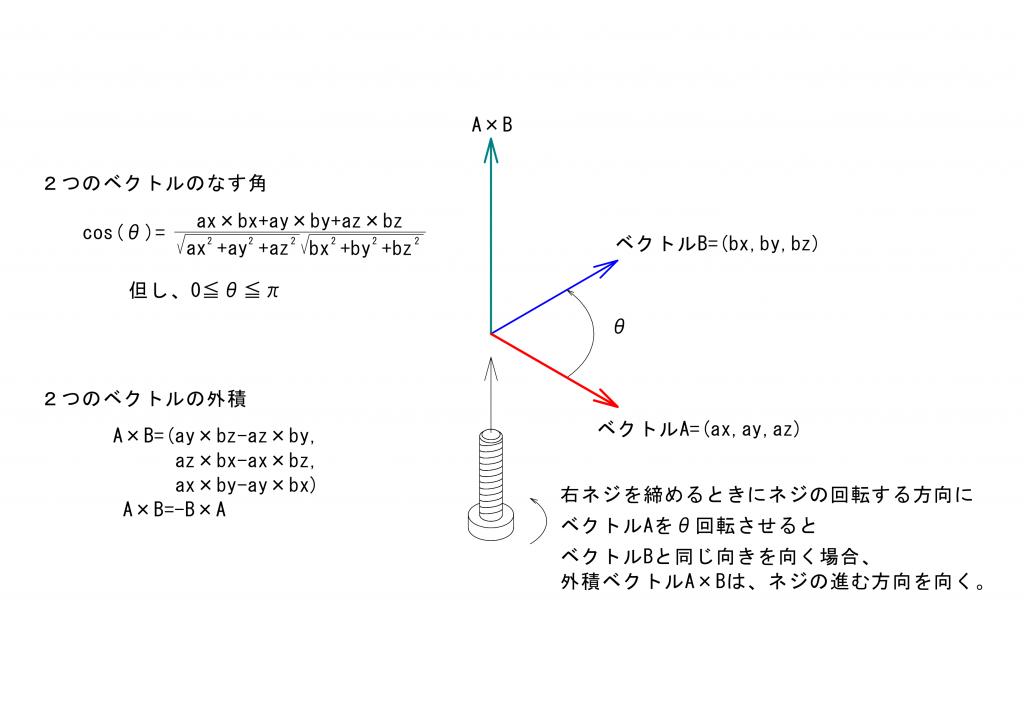
さて、ベクトル\(\vec{A}\)とベクトル\(\vec{B}\)とに垂直なベクトルの向きは3次元空間では2つ考えることができます。\(0<\theta<\pi\)となるような\(\theta\)角度だけ(右)ネジを締める方向にベクトル\(\vec{A}\)を回転させて、ベクトル\(B\)に重ねることができる場合を考えます。このネジが進む方向のベクトルが、外積ベクトルとなります。
あるいは、ベクトル\(\vec{A}\)とベクトル\(\vec{B}\)とを\(xy\)平面に置き、ベクトル\(\vec{A}\)を\(x\)軸の正の方向に向け、このベクトルを反時計回りに\(\theta\)回転させたときに、ベクトル\(\vec{B}\)に重ねることができる場合、外積ベクトル\(\vec{A}\times\vec{B}\)は、\(z\)軸の正の方向を向きます。
参考までに、ベクトル\(\vec{A}\)とベクトル\(\vec{B}\)とに垂直なもう一方のベクトルは、\(\vec{B}\times\vec{A}\)を計算すれば求めることができます。
なお、ベクトル\(\vec{A}\)とベクトル\(\vec{B}\)とが同じ方向を向き、\(\theta=0\)となる場合、およびベクトル\(\vec{A}\)とベクトル\(\vec{B}\)とが反対の方向を向き、\(\theta=\pi\)となる場合は、二つのベクトルの外積\(\vec{A}\times\vec{B}\)は\(0\)ベクトル\((0, 0, 0)\)となります。
また、外積ベクトルの長さは2つのベクトルがなす平行四辺形の面積に等いという重要な性質がありますが、今回はこの性質は使いませんので、以下では触れませんが、この性質を式で表すと、
\(|\vec{A}\cdot\vec{B}| = |\vec{A}|\cdot|\vec{B}|\cdot sin(\theta)\)
ここまで述べたことを簡単に絵にまとめました。