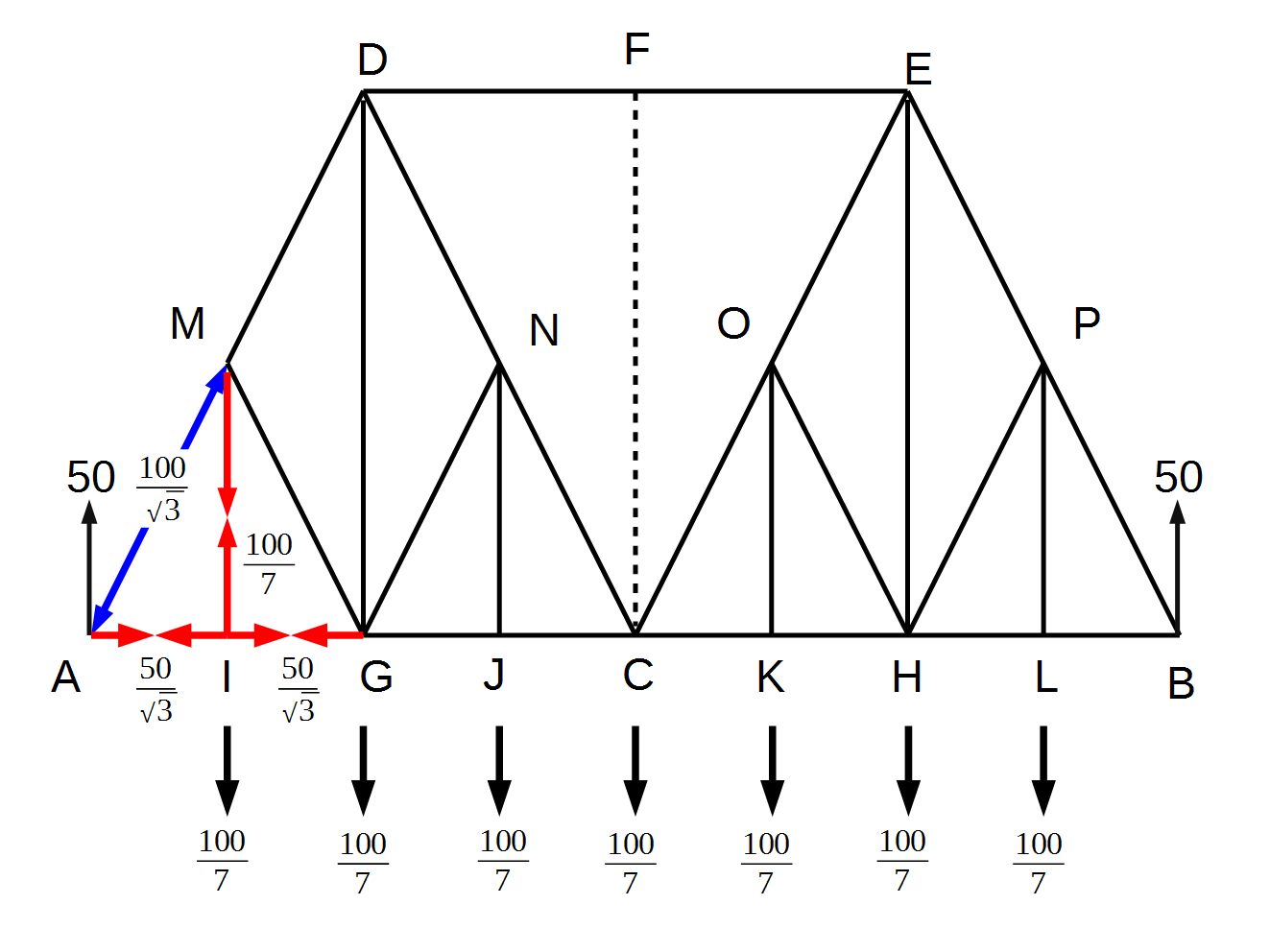
前回同様の、橋の下部のすべての節点に均等に力が加わる場合をBaltimore Truss Bridgeで考えてみます。下図のとおり、I、G、J、C、K、H、Lの各店に下向きに(\frac{100}{7})の力が加わるとします。
これまでの計算どおり、A点、B点のそれぞれに上向きの50の力が加わります。M-A、A-Iの力はこの上向きの力から計算することができます。M-Iの部材のI点には、下向きの(\frac{100}{7})を打ち消す力が働きます。また、I-Gの部材のI点には、A-Iの部材のA点を打ち消す力が働きます。これらを表現したのが下図です。
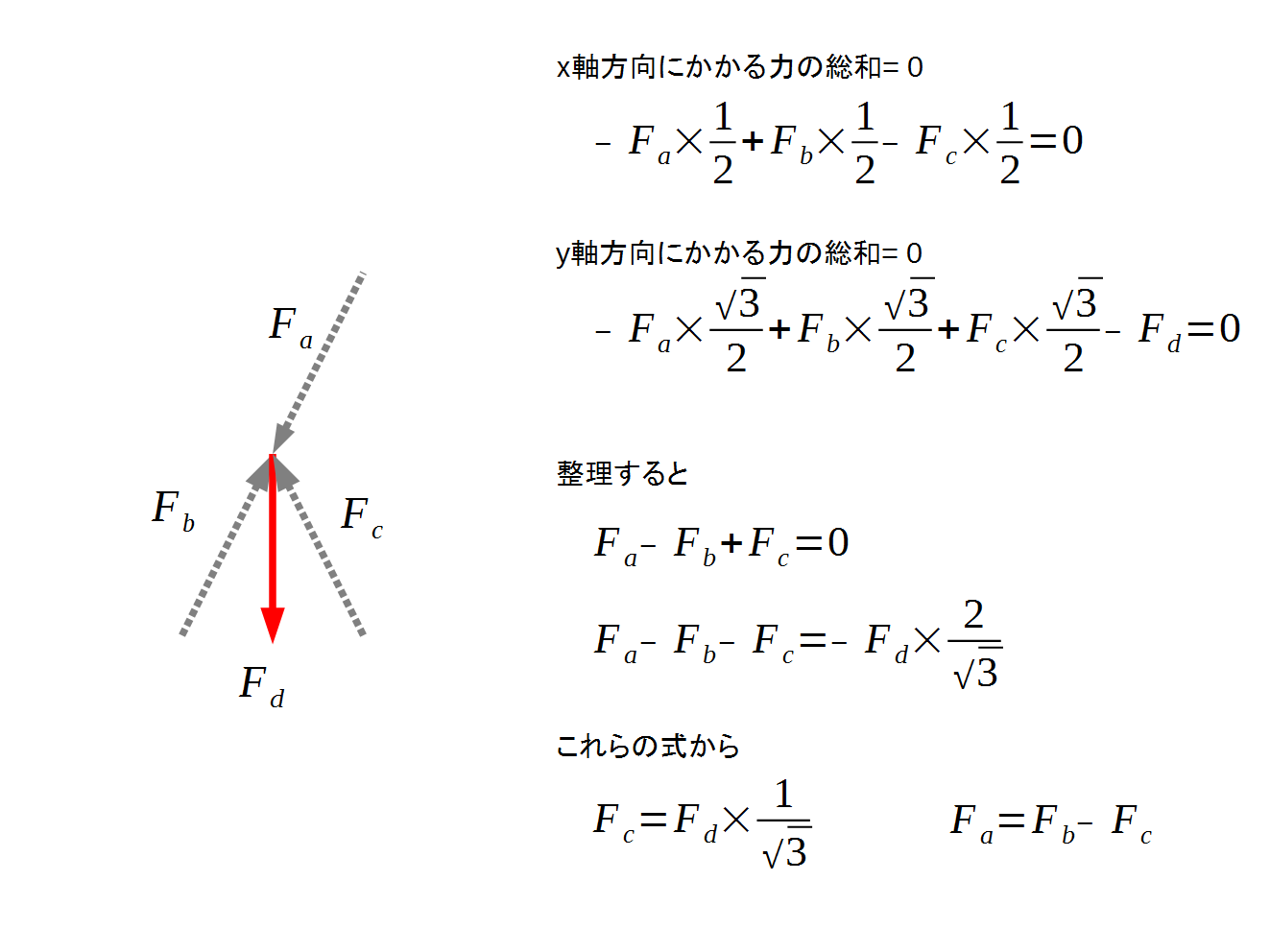
ここで、M点のような、Baltimore Trussに特有の、小さなトラス構造の頂点にどのような力が加わるかを一般化して解いてみます。
ここから、Baltimore Truss Bridgeの小さなトラス構造の縦の部材に下向きの力がかかった場合、その(\frac{1}{\sqrt{3}})の力(注:斜材の角度が60度のとき)が、小さなトラス構造を構成する斜材に斜め上向きにかかる、ということがわかります。
また、大きなトラス構造の斜材の上半分には、その下半分にかかる力から上で計算した小さなトラス構造の値を引いた大きさの力が、反対向きにかかる、ということがわかります。
ただし、これは、大きなトラス構造の斜材に関して、下半分からは斜め上向きの力が、上半分には斜め下向きの力が加わる、という前提ですので、もしも向きが反対であれば、符号を反転する、引き算をした結果、符号が反転したら、向きを反転させる、といったことが必要です。
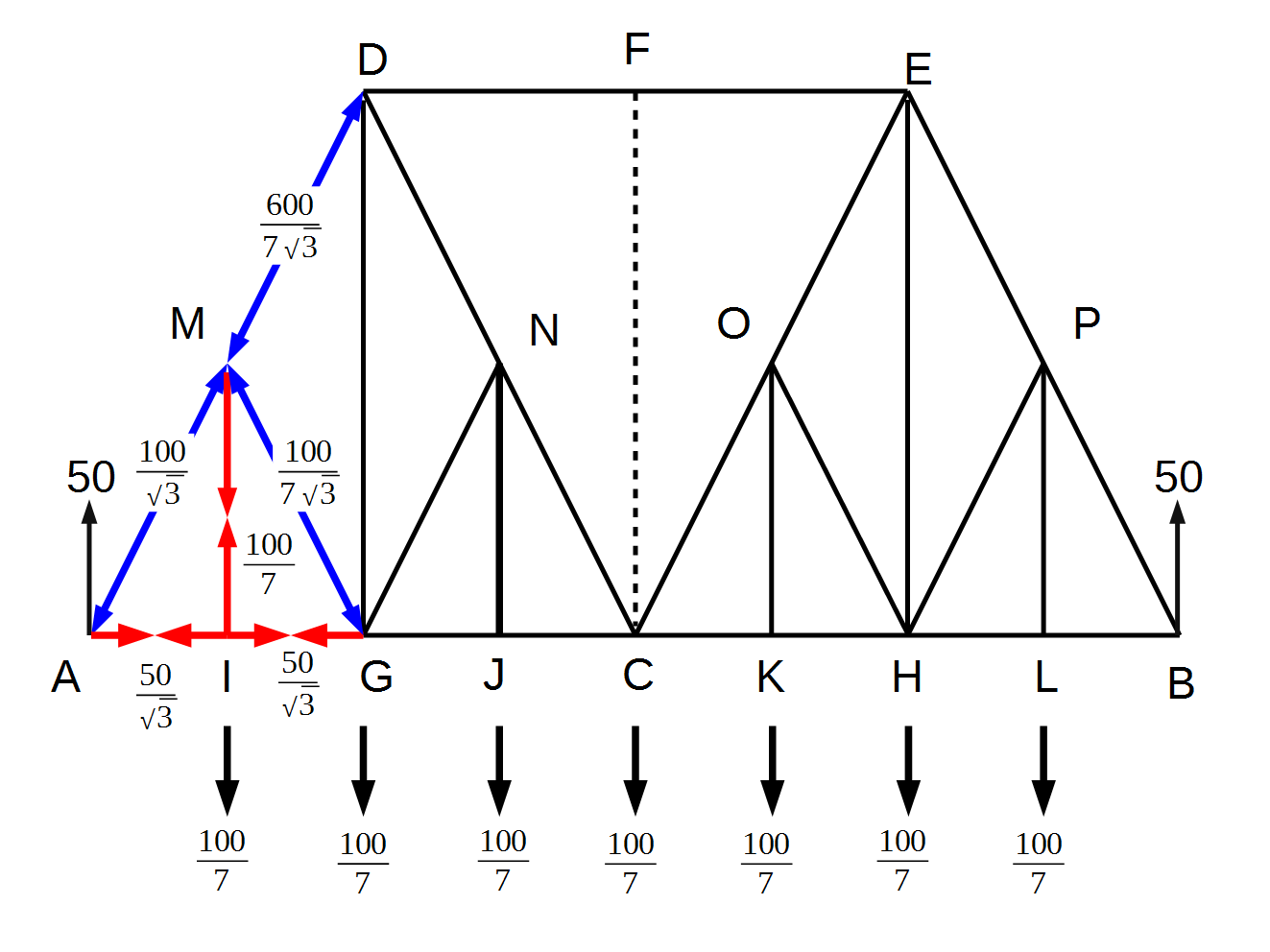
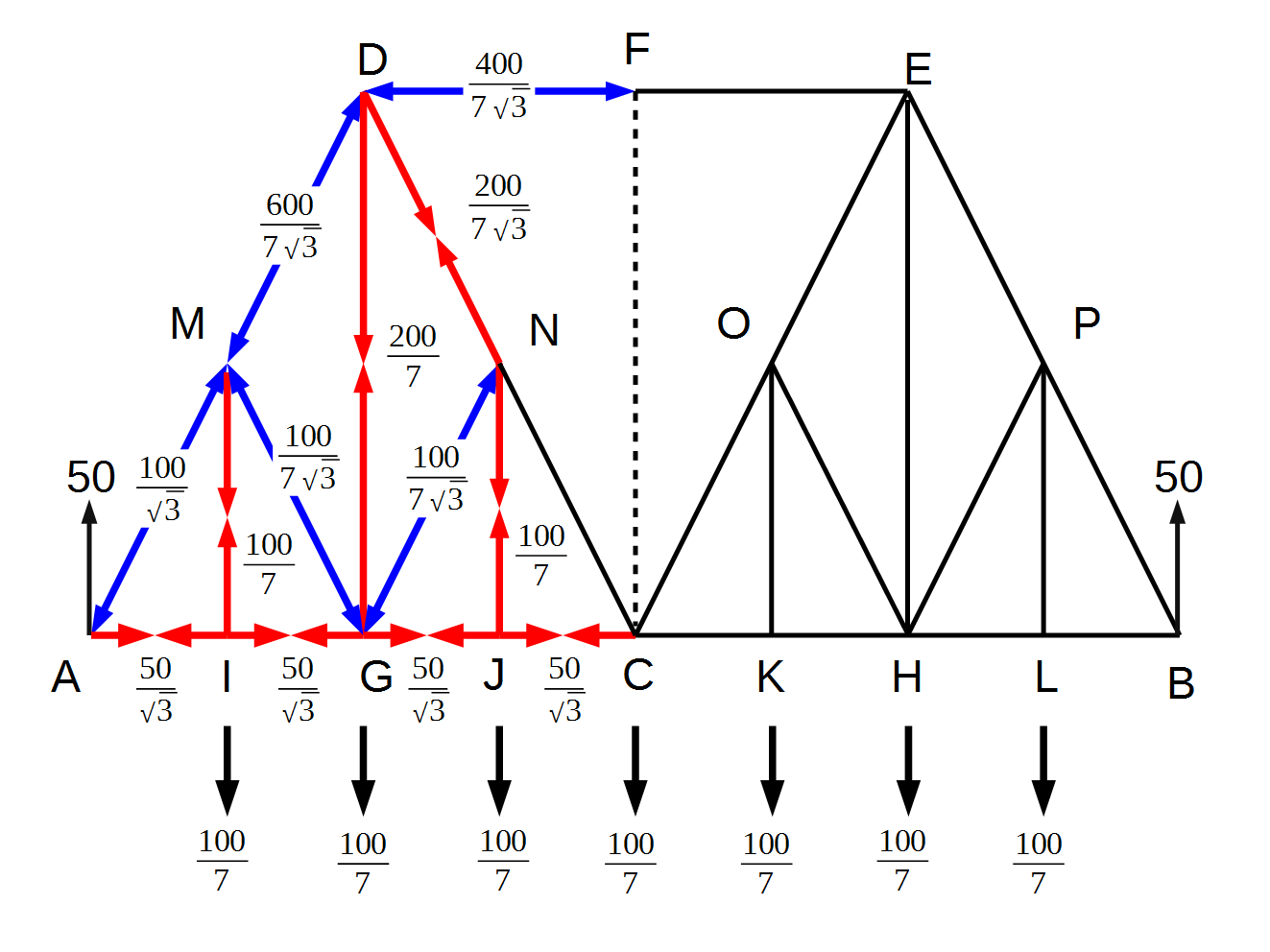
この結果をもとに計算結果を記入したのが下図です。
次に注目するのがN-Jの部材です。J点には下向きに(\frac{100}{7})の力がかかりますので、N-Jの部材のJ点には上向きの(\frac{100}{7})の上向きの力が、N点には(\frac{100}{7})の下向きの力が加わります。
上で求めた通り、N-Gの部材のN点には、斜め上向きの(\frac{100}{7\sqrt{3}})の力が加わります。ここまでを表現したのが下図です。
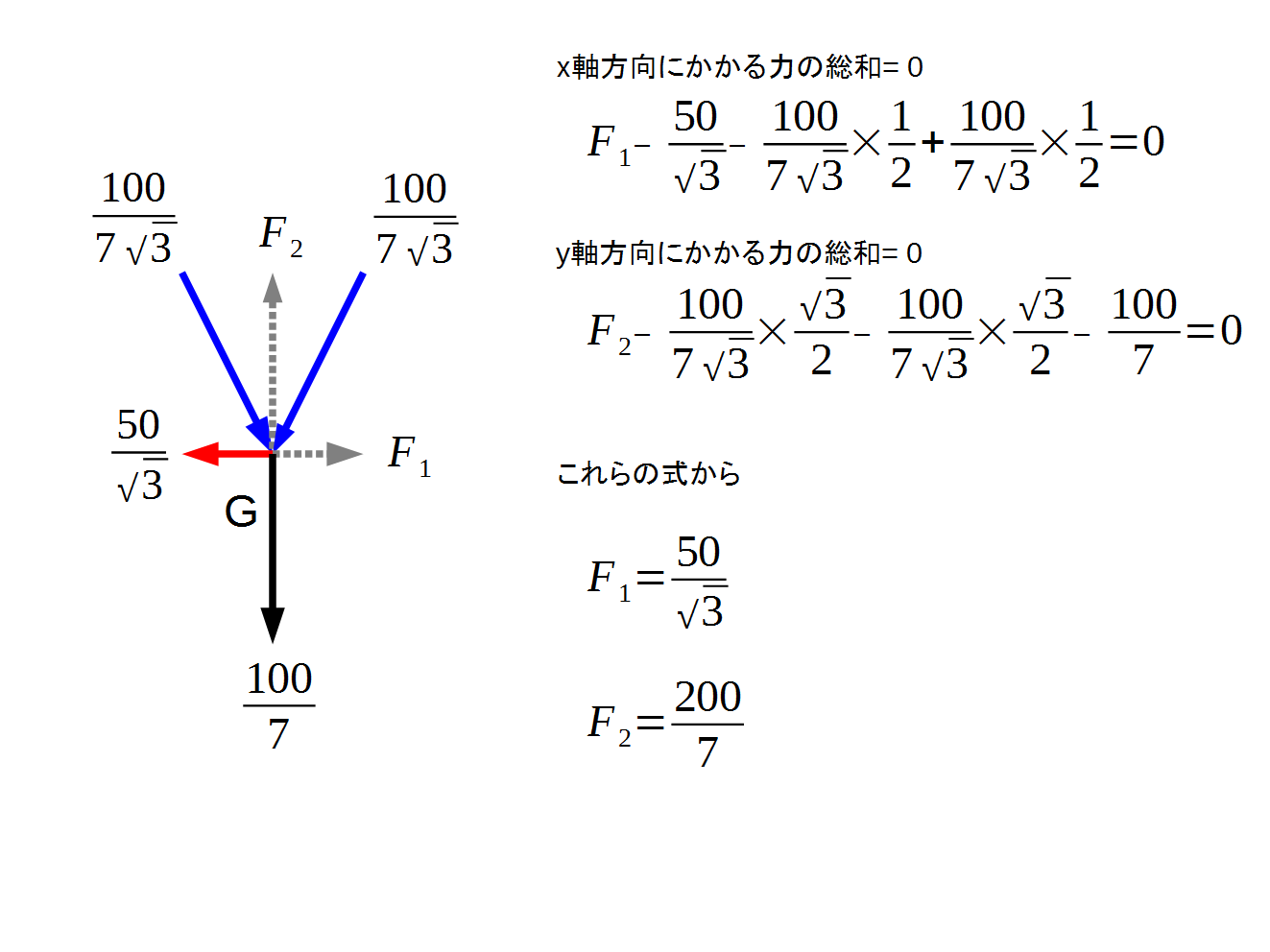
ここまでくると、G点にかかる力を次のように解くことができます。
ここまでの結果を書き込みます。
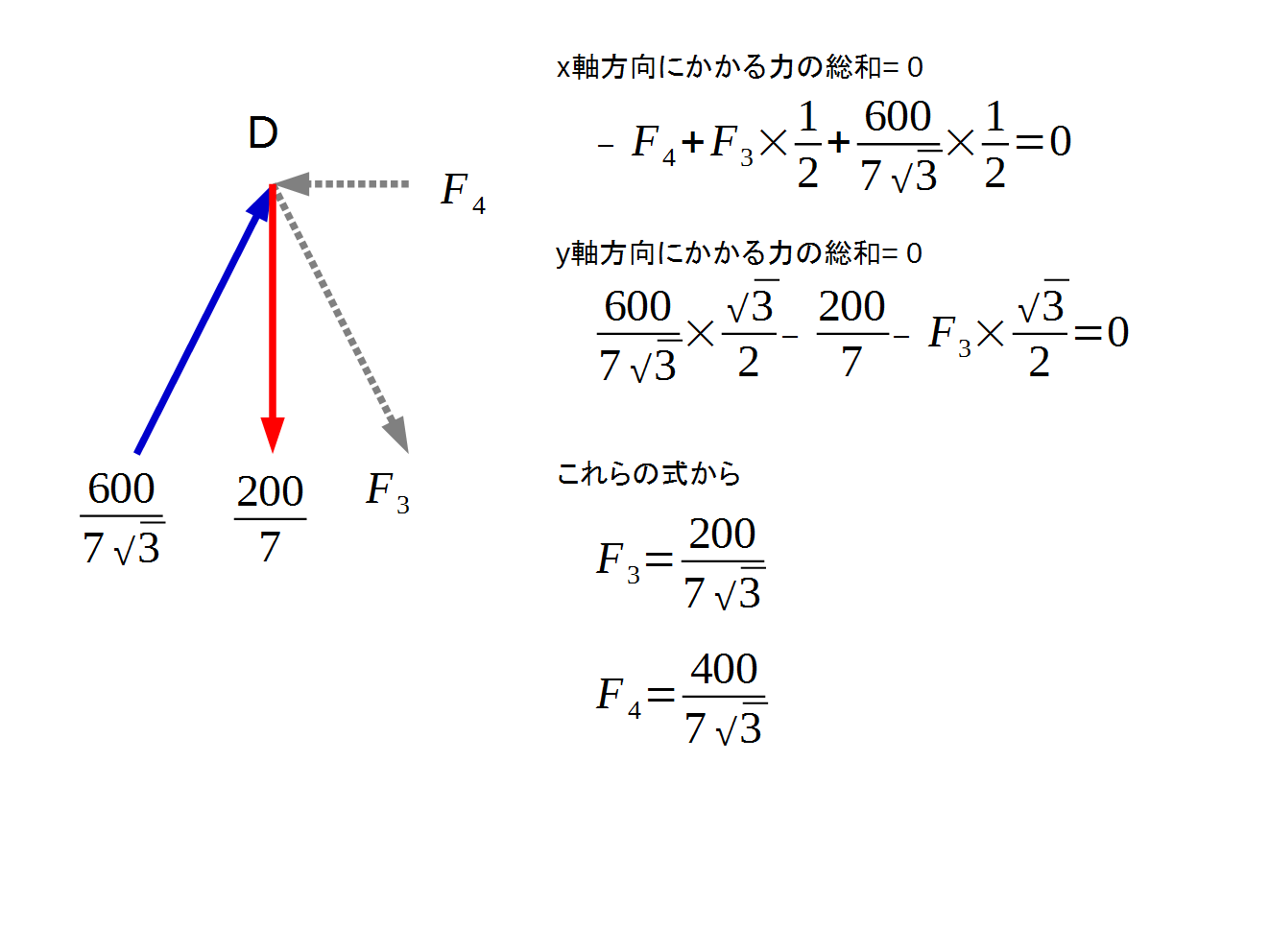
次はD点に注目して、かかる力を計算します。
この結果を追加したのが次の図です。
上で解いたBaltimore Truss Bridgeの小トラスの頂点の力のかかり方の一般解から、N-Cにかかる力を求めます。N点に左斜め上からかかる力に、Nの小トラスの斜材にかかる力を加えればよいのですが、Nから左斜め上に(\frac{200}{7\sqrt{3}})の力が加わっていますので、これはN点に左斜め上から(-\frac{200}{7\sqrt{3}})の力が加わると考えます。これに(\frac{100}{7\sqrt{3}})を加えると、Nに向けて右斜め下から(-\frac{100}{7\sqrt{3}})の力が加わることになります。これを言い換えると、Nから右斜め下に(\frac{100}{7\sqrt{3}})の力が加わる、ということです。
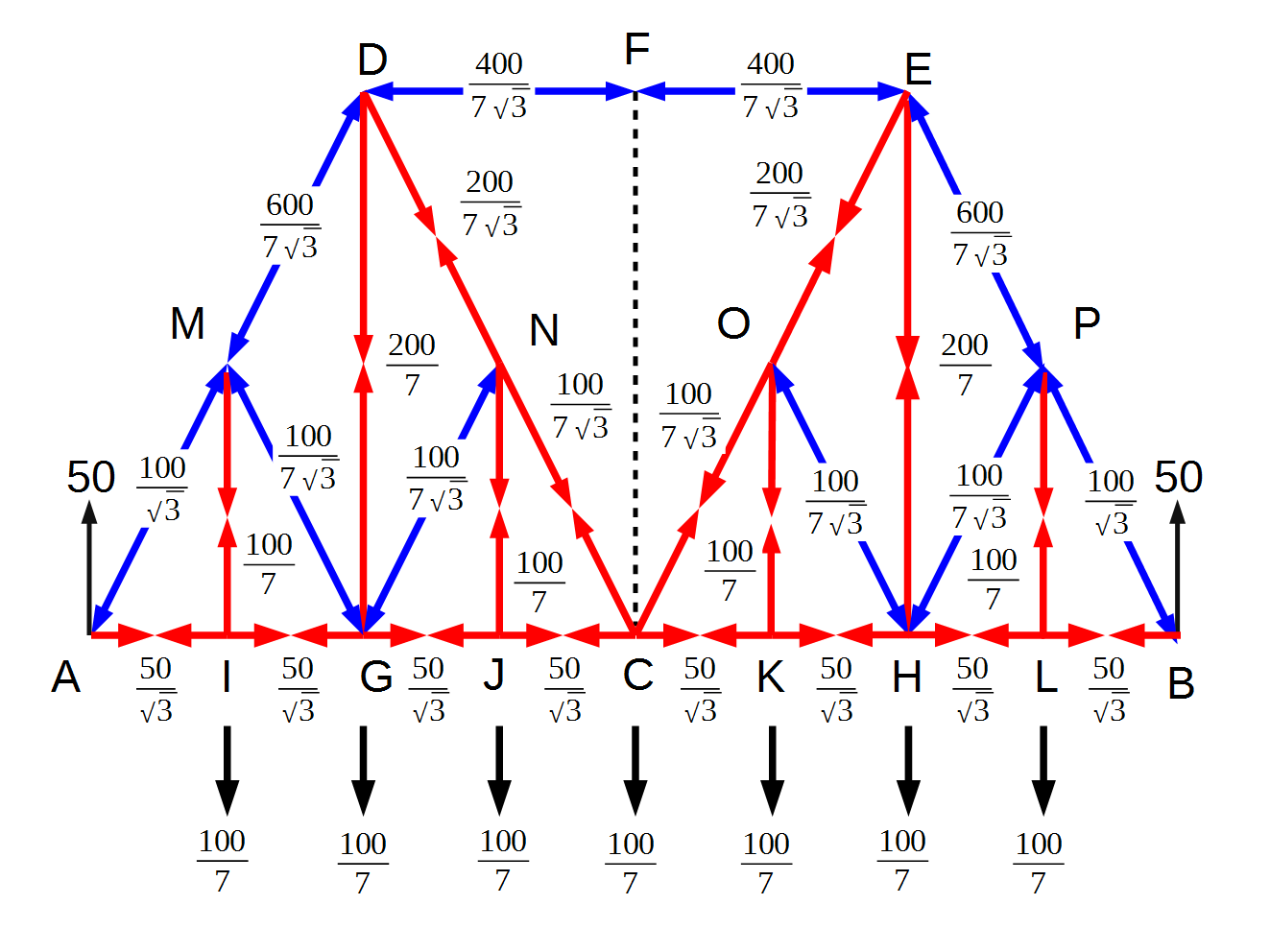
何やら面倒くさそうな計算に思えますが、じっと矢印の方向を見ると、簡単に計算できるようになります。この結果を加え、右側にも対称に結果を加えたのが次の図です。
少々わかりにくいので、分数を計算して、最終的に次が得られます。