今回より、橋の構造部材にかかる力の計算の具体例を何回かに分けて取り上げてゆきます。
なお、話を簡単にするために、以後のすべての議論において、力のかかるのは節点のみとします。また、計算を簡単にするために、斜材の角度はすべて60度とします。したがって、
(cos(60^\circ) = \frac{1}{2} )
(sin(60^\circ) = \frac{\sqrt{3}}{2} )
となります。
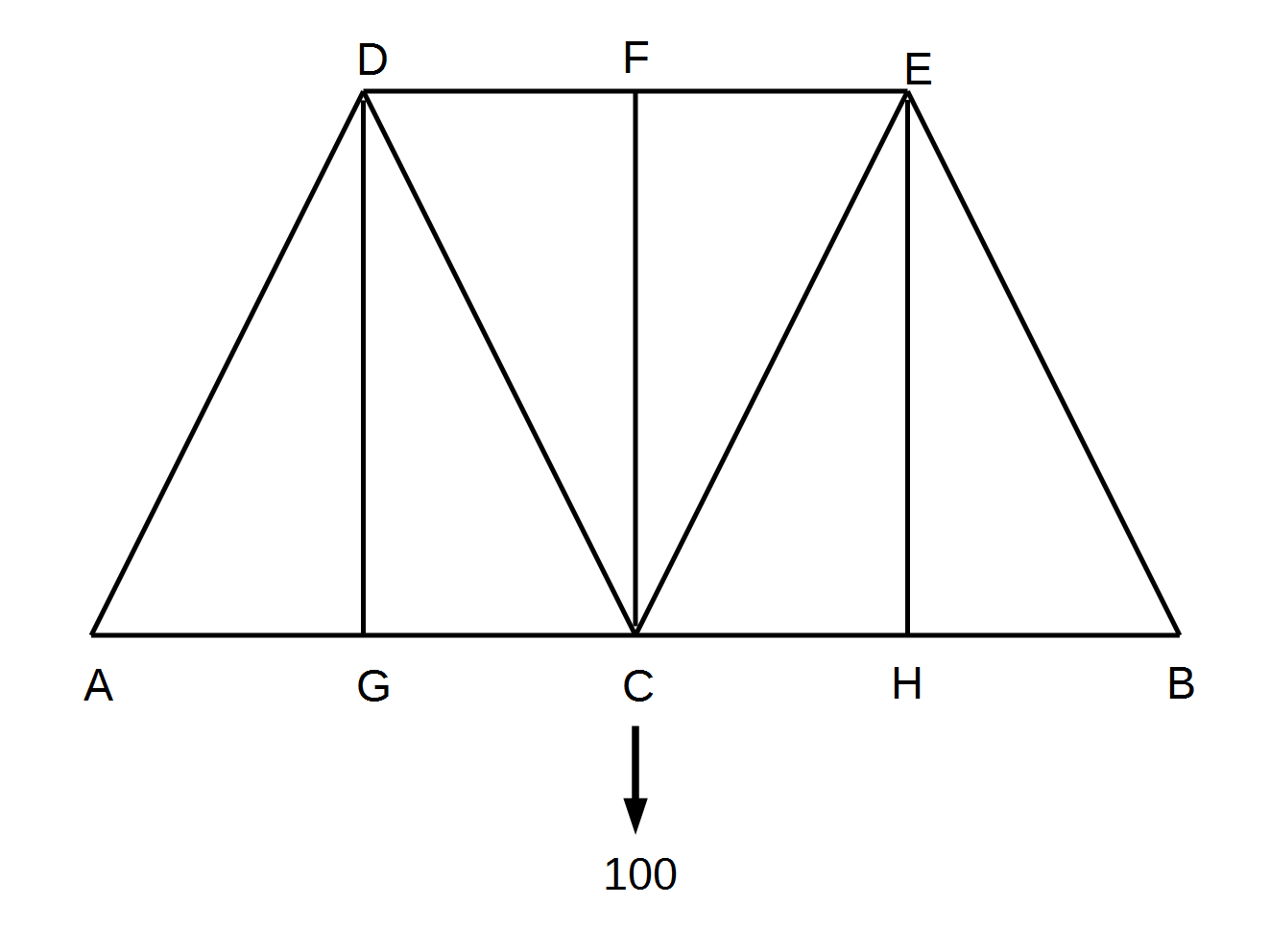
例題として使うのは、前回の説明で使った4パネルのPratt Truss Bridgeです。下辺の中心に100の力が加わるものとします。
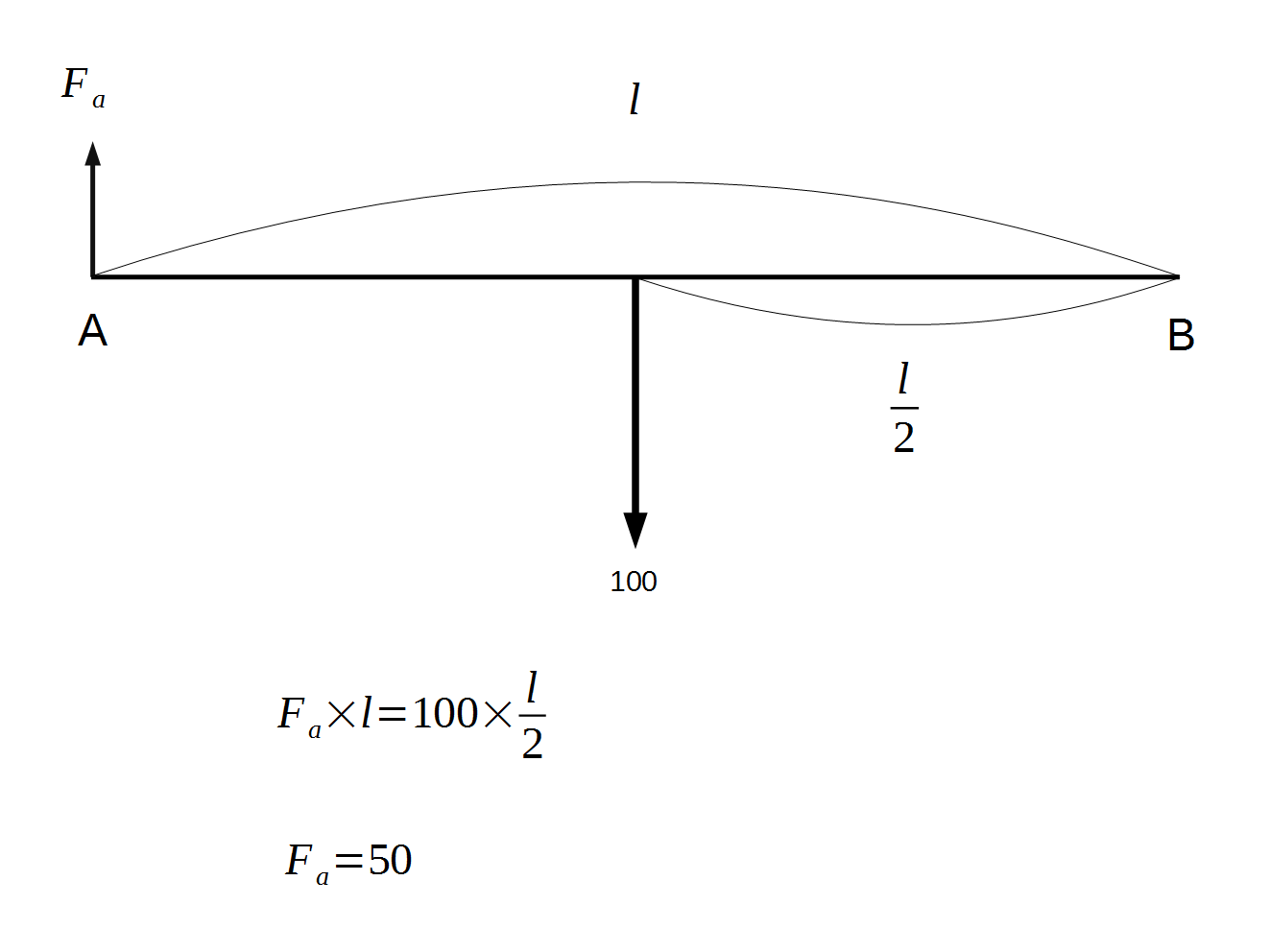
どの計算でも、最初に行うべきことは橋の両端(支承)にかかる力を計算することです。B点を支点とすると、Cに加わる100の力を打ち消す力がA点にかかることとなります。これは梃子の原理で下のとおり簡単に計算ができます。
同様にA点を支点としてB点に加わる力を計算すると、同じく(50)となります。
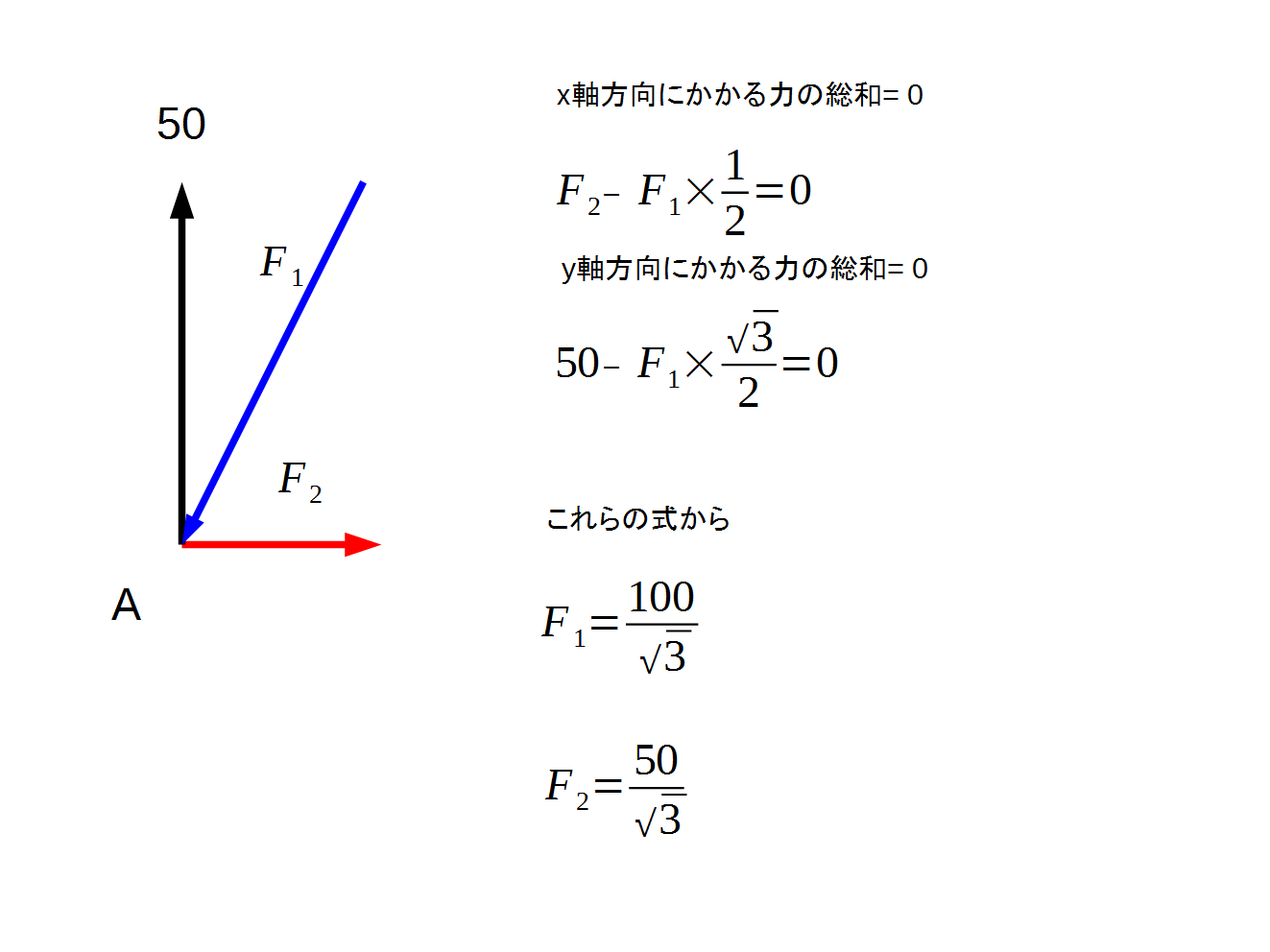
これらの力がわかると、A点とB点との構造部材にかかる力を計算することができます。下図はA点にかかる力を計算したものです。
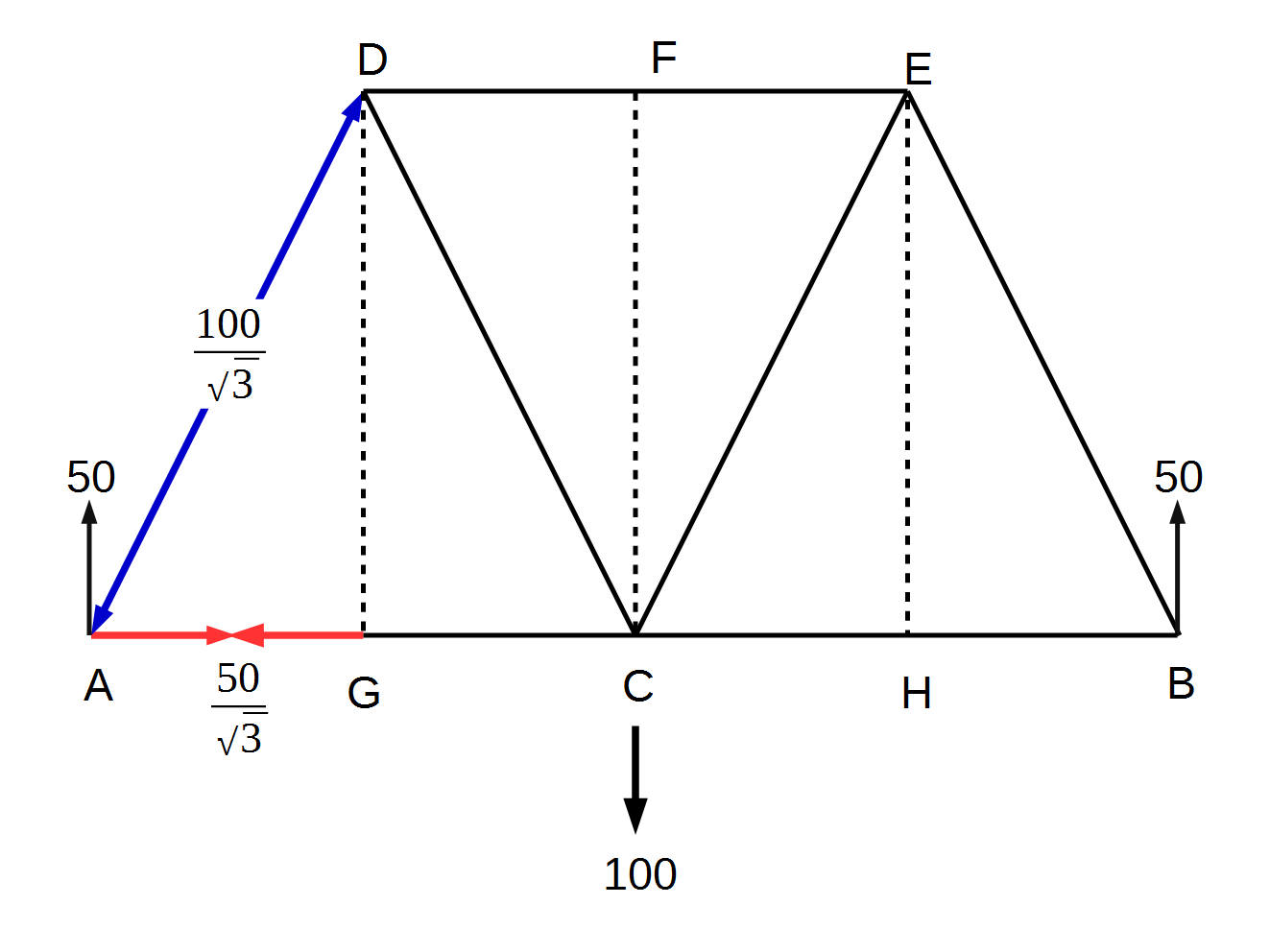
前回説明した通り、A-Dの構造材に注目すると、A点にかかる力と反対向きの力がD点にかかります。同様に、B点にかかる力と反対向きの力がG点にかかります。これらを記入したのが次の図です。
ここで、Zero Force Memberの説明をします。これは、力の全くかからない、圧縮でも伸張でもない部材のことで、上の図で点線とした、D-G、F-C、E-Hが相当します。G点に注目すると、垂直方向に力が発生する可能性があるのは、D-Gの部材のみであり、G点にかかる力が発生しても、それを打ち消して垂直方向の力の総和を(0)とする力が存在しません。したがって、G点には力が発生せず、D-Gの構造材には力がかからないことになります。F点、F点についても同様です。
紛らわしいのはC点で、Cに下向きに(100)の力がかかっているので、F-Cの構造材に力がかかりそうな気がしますが、上記の議論でF点には力がかかることはありえないので、F-Cの構造材には力がかかりません。したがって、Cにかかる下向きの力を打ち消す力は、D-C、E-Cの斜材で発生することとなります。
次にD点に注目すると、下図のように簡単に計算できます。
ここまでの結果を反映したのが下の図です。これで左半分の力のかかり方がわかりました。
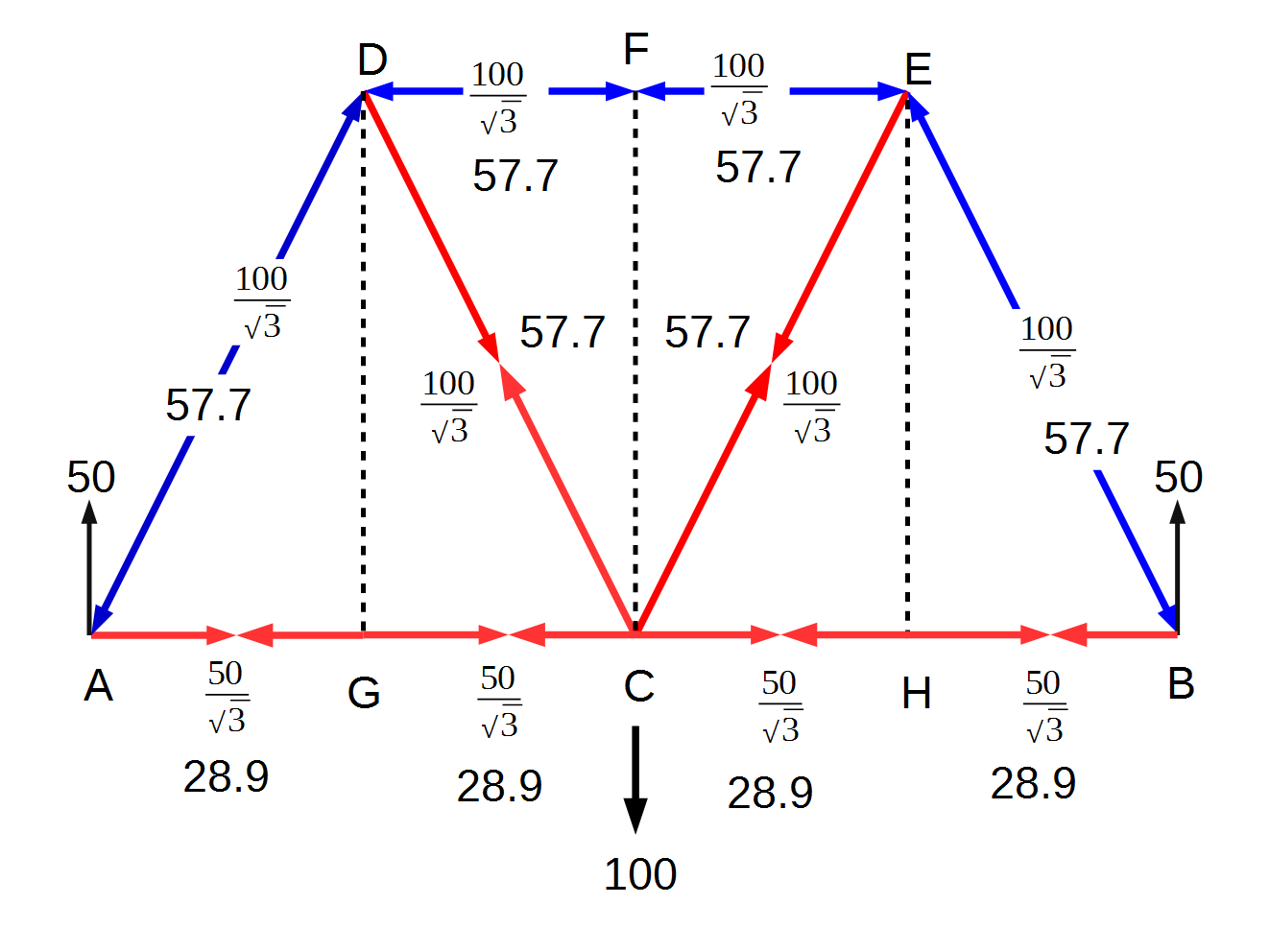
この橋の力のかかり方は、左右対称なので、右側にも同じ数字が対象に入ります。最終的に次のような結果となります。
念のために、C点の力の総和が(0)になることを検算します。
次回は、4パネルのBaltimore Trussで同様の計算を行ってみます。